LFSR Properties & Tests

LFSR Properties:: Test 3+1 properties of LFSR

Using test_properties(verbose=1) method, it we can test if LSFR set be state and polynomial setisfies the following properites in addition to periodicity (period T = 2^M -1) for M-bit LFSR * (1) Balance Property * (2) Runlength Property * (3) Autocorrelation Property

Test LFSR [5,3], for 5-bit LFSR, which we know is a primitive polynomial

state = [1,1,1,1,0]
fpoly = [5,3]
L = LFSR(initstate=state,fpoly=fpoly)
result  = L.test_properties(verbose=2)

1. Periodicity
------------------
 - Expected period = 2^M-1 = 31
 - Pass?:  True

2. Balance Property
-------------------
 - Number of 1s = Number of 0s+1 (in a period): (N1s,N0s) =  (16, 15)
 - Pass?:  True

3. Runlength Property
-------------------
 - Number of Runs in a period should be of specific order, e.g. [4,2,1,1]
 - Runs:  [8 4 2 1 1]
 - Pass?:  True

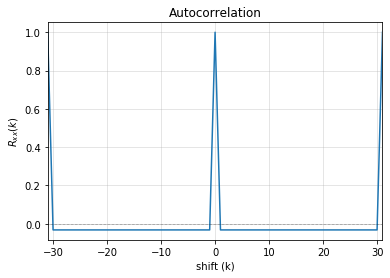
4. Autocorrelation Property
-------------------
 - Autocorrelation of a period should be noise-like, specifically, 1 at k=0, -1/m everywhere else
 - Pass?:  True


==================
Passed all the tests
==================

Test LFSR [5,1], for 5-bit LFSR, which we know is *NOT* a primitive polynomial

state = [1,1,1,1,0]
fpoly = [5,1]
L = LFSR(initstate=state,fpoly=fpoly)
result  = L.test_properties(verbose=2)

1. Periodicity
------------------
 - Expected period = 2^M-1 = 31
 - Pass?:  False

2. Balance Property
-------------------
 - Number of 1s = Number of 0s+1 (in a period): (N1s,N0s) =  (17, 14)
 - Pass?:  False

3. Runlength Property
-------------------
 - Number of Runs in a period should be of specific order, e.g. [4,2,1,1]
 - Runs:  [10  2  1  1  2]
 - Pass?:  False

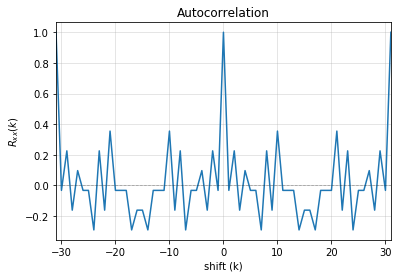
4. Autocorrelation Property
-------------------
 - Autocorrelation of a period should be noise-like, specifically, 1 at k=0, -1/m everywhere else
 - Pass?:  False

==================
Failed one or more tests, check if feedback polynomial is primitive polynomial
==================

Test individual properties

state = [1,1,1,1,1]
fpoly = [5,4,3,2]
L = LFSR(initstate=state,fpoly=fpoly)

# get one full period
p = L.getFullPeriod()

L.balance_property(p.copy())
L.runlength_property(p.copy())
L.autocorr_property(p.copy())

+

Feedback (Primitive) Polynomials:

A primitive polynomial is is irreducible, and not trivial to derive. A list of primitive polynomials upto 32 degree can be found at Ref, which is not an exhaustive list. Since for each primitive polynomial, an image replica (which is also primitive) can be computed easily list include half of polynomials for each degree and other half can be compputed by get_Ifpoly() method, see example 7.2

Ref : http://www.partow.net/programming/polynomials/index.html

Get a list of feedback polynomials for a m-bit LFSR

import pylfsr as PYL
PYL.get_fpolyList(m=5)
[[5, 2], [5, 4, 2, 1], [5, 4, 3, 2]]

# list of all feedback polynomials as a dictionary
fpolyDict = PYL.get_fpolyList()

Or optional way, if LFSR object is already in place

from pylfsr import LFSR

L = LFSR()
# list of 5-bit feedback polynomials
fpolys = L.get_fpolyList(m=5)
[[5, 2], [5, 4, 2, 1], [5, 4, 3, 2]]

# list of all feedback polynomials as a dictionary
fpolyDict = L.get_fpolyList()

Get a image replica of a feedback polynomial

Image replica of a primitive polynomial is a primitive polynomial, hence a valid feedback polynomial for LFSR For m-bit primitive polynomial p(x) = x^m + x^k + .. + 1, a image replica is ip(x) = x^(-m)p(x) where 0 < k < m

L = LFSR()
L.get_Ifpoly([5,3])
[5, 2]

L.get_Ifpoly([5,4,3,2])
[5, 3, 2, 1]

import pylfsr as PYL
PYL.get_Ifpoly([5,4,3,2])
[5, 3, 2, 1]

Changing feedback polynomial in between

After generating some bits from an LFSR, a feedback polynomial can be changed keeping the current state as intial state and generate the new sequece.

L = LFSR(fpoly=[23,18],initstate ='ones')
seq0 = L.runKCycle(10)

# Change after 10 clocks
#L.changeFpoly(newfpoly =[23,14],reset=False)
L.set_fpoly(fpoly =[23,14],reset=False)
seq1 = L.runKCycle(20)

# Change after 20 clocks
L.set_fpoly(fpoly=[23,9],reset=False)
seq2 = L.runKCycle(20)

Changing configuration in between

L = LFSR(fpoly=[23,18],initstate ='ones',conf='fibonacci')
seq0 = L.runKCycle(10)

# Change after 10 clocks
L.set_conf(conf='galois',reset=False)
seq1 = L.runKCycle(20)